La compartimentación del espacio era el título un tanto vago de aquella tesis, que pudo llamarse con más precisión (y también ampulosidad) "divisiones regulares del espacio, según sistemas de simetría, en recintos repetitivos por traslación, reflexión y rotación".
Puede verse un resumen de su contenido en este enlace. y consultarse completa en la biblioteca da Universidade da Coruña y en su repositorio.
Para descargarla en PDF escaneado del texto original, dejo estos enlaces:
Tomo I
Tomo IIComo podréis observar, el texto es de lo más artesanal. Mi querida compañera en estas (y muchas otras) fatigas se encargó de su difícil mecanografía con una vieja máquina y mucha paciencia, la misma que tuve para sus dibujos hechos directamente a mano. Aún la informática no había llegado a nuestra casa.
Lo más esencial de su contenido se sintetiza en esos esquemas.
Para abrir boca sobre una curiosa propiedad de las redes regulares, tanto planas como espaciales (la dualidad) dejo aquí un ejemplo.
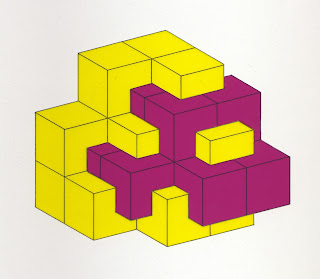
El sistema más simple y universal para dividir el espacio es el cúbico. Obsérvese esta macla de cubos:
Los cubos de cada color tienen sus vértices en los centros de los cubos del otro. Imaginemos que en los vértices de los cubos amarillos surgen pequeños octaedros violeta que crecen devorándolos. Un nuevo espacio va sustituyendo al primero, a través de fases en las que aparecen nuevos poliedros del sistema. Se trata de poliedros semirregulares.
Estos poliedros tienen idénticos sus vértices y aristas y sus caras son regulares, pero pertenecen a dos grupos distintos: en primer lugar aparecen triángulos y octógonos.
También son distintos los poliedros de la malla conjunta, salvo en un caso.
Primero aparecen caras triangulares y octogonales en los mermados cubos amarillos, que se convierten en cubos truncados. Luego, estos mismos cubos menguan hasta convertirse en cuboctaedros de caras triangulares y cuadradas. Los espacios amarillos y violetas se equilibran cuando aparecen los octaedros truncados de caras exagonales y cuadradas. Y el proceso continúa, invirtiendo los espacios hasta que desaparece el amarillo, sustituido por una malla de cubos violeta.
Este octaedro truncado, o poliedro de Kelvin, es el único poliedro semirregular capaz de llenar el espacio por sí solo. Como hemos visto, al superponerlo a la red cúbica nos damos cuenta de que pertenecen a dos familias en pugna, y que las caras exagonales son los frentes de batalla. Lo que no se aprecia en esta imagen, en que se han coloreado sin otro criterio que evitar la vecindad de dos espacios del mismo color.
Este poliedro optimiza el apilamiento de celdas iguales, porque minimiza la superficie de las caras. Si esas pirámides de balas de cañón esféricas que tanto gustan colocar en la puerta de los cuarteles de artillería fueran compresibles y tuvieran que rellenar sus huecos, adoptarían esa forma. ¿No os recuerda la disposición de los granos de una granada? (de las de comer, no de las de explotar).
(sigue)








No hay comentarios:
Publicar un comentario