Una tesis geométrica. Compartimentación simétrica del espacio

Se inicia aquí la segunda parte de la tesis que estoy comentando.

El primer capítulo de esta parte, y séptimo del total, puede descargarse aquí.

La primera parte comprendía el estudio de poliedros regulares y semirregulares aislados. La propiedad que compartían ambas categorías era la identidad de todos sus vértices. Cuando la suma de ángulos concurrentes en ellos era inferior a 360º, teníamos poliedros convexos, pero si se alcanzaba esa cifra se convertían en mosaicos planos.

Estos mosaicos llenaban el plano repitiendo indefinidamente una combinación de polígonos que mantenían la identidad de todos los vértices. Traspasando esta propiedad al espacio tridimensional, ¿se lo puede llenar con poliedros que compartan vértices idénticos en una repetición infinita?

La respuesta es afirmativa, y ese es el tema que se aborda en esta segunda parte.

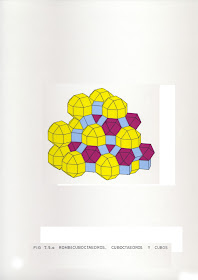
Como para muestra basta un botón, aquí tenemos un conglomerado espacial que incluye cubos (4,4,4), cuboctaedros (3,4,3,4) y rombicuboctaedros (3,4,4,4). Cada cubo está en contacto con cuatro rombicuboctaedros y dos cuboctaedros, el cuboctaedro confina con seis cubos y ocho rombicuboctaedros, los cuales a su vez están en contacto con doce cubos, ocho cuboctaedros y seis poliedros de su misma clase:

De estructura muy semejante es esta agrupación de cubos (4,4,4), octaedros truncados (4,6,6) y grandes rombicuboctaedros (4,6,8). que se limitan unos a otros de la misma forma que los anteriores. En ambos casos, el poliedro de mayor tamaño gobierna los espacios limítrofes, pues resulta de un gran cubo cuyas doce aristas y ocho vértices han sido recortados, y los espacios vacíos resultantes son rellenados por cubos en las doce aristas eliminadas y otros poliedros en los ocho vértices, mientras mantienen contacto por sus caras con otros seis de su clase:

Una de las formas más sencillas de obtener estas mallas la expuse aquí. El truncamiento de la malla se limitaba a los vértices, y progresivamente iba invadiendo los cubos originales hasta llegar a su supresión total, momento en que la malla era sustituida por otra dual: los centros de los nuevos cubos se situaban en los vértices de los originales, y viceversa.

Otra malla espacial la forman tetraedros (3,3,3) y octaedros (3,3,3,3). Los octaedros entran en contacto por sus aristas y vértices, y los tetraedros ocupan los espacios contiguos a las caras, de modo que las caras en contacto nunca pertenecen a poliedros iguales. A su vez, los tetraedros entran en contacto por sus aristas, con dos posiciones, de forma que los de la misma posición sólo se relacionan por sus vértices:

Estos son los octaedros de la red:

Los tetraedros de la clase I:

Tetraedros de la clase II:

La estructura que resulta al materializar la malla mediante barras resistentes a tracción y compresión en las aristas, con nudos en los vértices, es de una gran solidez. Por eso es utilizada para construir estructuras espaciales que logran cubrir grandes superficies sin soportes intermedios. Este enlace os devolverá a un artículo que dediqué al Pabellón de los Deportes de Pontevedra, obra de Alejandro de la Sota, lugar al que voy a menudo a hacer gimnasia. En la última fotografía puede apreciarse la estructura de cubierta, constituida por medios octaedros limitados por tetraedros en dos posiciones.

Esta otra malla, muy semejante, la forman tetraedros (3,3,3) y tetraedros truncados (3,6,6). Estos últimos, por su menor simetría, aparecen ahora en dos posiciones, a diferencia de los octaedros en la malla anterior. La semejanza de ambas redes se deduce de las descomposiciones del hexaedro rómbico que ya expuse en este otro lugar.

Esta es la red compacta:

Eliminando los tetraedros:

Tetraedros truncados de la clase I:

Tetraedros truncados de la clase II:

Tetraedros, en contacto sus vértices:

Finalizo con esta malla de octaedros truncados (4,6,6), tetraedros truncados (3,6,6) de dos clases y cuboctaedros (3,4,3,4). En ella las caras en contacto pertenecen siempre a poliedros de distinta clase. Los cubos truncados quedan aislados entre sí, mientras los cuerpos de cada una de las otras clases toman contacto por las aristas:

Basta por ahora. Continuará.

(sigue)