Vuelvo a lamentar la poca fidelidad de las imágenes, en las que no se aprecian bien las líneas más finas. En todo caso, si ya no lo habíais hecho, podéis descargar el PDF en el que se aprecian mucho mejor, sobre todo si se amplía la imagen.
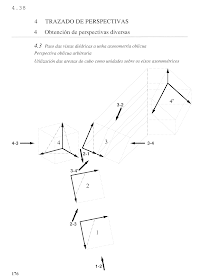
Estos cubos de oro pueden servir de homenaje a este poliedro, verdadera unidad del espacio. Vamos a ver como, partiendo de sus simplicísimas vistas en planta y alzado, podemos colocarlo en la posición que queramos, con dos movimientos de rodadura, girando en cada uno un ángulo de 90º, obteniendo una perspectiva paralela, o axonometría.
Moviéndonos en sentido inverso, veremos que, dados los ángulos que forman entre sí los ejes de una perspectiva axonométrica, podemos llegar a las vistas canónicas, planta y alzado, y establecer las escalas y las verdaderas magnitudes de tal perspectiva.
Aún hay más: podremos obtener, conocida la posición del cubo y del punto de vista respecto al plano de proyección, cualquier clase de perspectivas centrales o cónicas. Así que ¡adelante!
La primera visual añadida a las vistas 1 y 2 iniciales, 2-3, coloca de canto en 3 las caras que estaban de frente en 2. La segunda 3-4 coloca oblicuamente todos los elementos en 4. Fijémonos, si la vista nos alcanza, y si no recurriendo al citado PDF, en un plano de canto perpendicular a 3-4 que pasa por el vértice más alto de la vista 3. Naturalmente estará de frente en 4. Este plano corta a tres caras del cubo en un triángulo llamado "triángulo de las trazas", porque sus lados son las trazas o inersecciones de los planos de esas caras con el plano en cuestión. Si suponemos que ese plano es el del dibujo, un vértice quedará tras él, y el resto de la figura delante. Si imaginamos que es una superficie acuática, el vértice quedará sumergido.
El triángulo de las trazas tiene sus lados perpendiculares a las proyecciones de las aristas del cubo.
Podemos entonces proceder a la inversa. Si partimos de la vista 4, trazamos desde un vértice (el más alto, por ejemplo) perpendiculares a las otras aristas, y así obtenemos el susodicho triángulo de las trazas. Como 4-3 es la dirección de uno de sus lados, este movimiento lo pondrá en 3 de punta, y de canto la cara que lo contiene. Elegida la dirección 3-2 para la siguiente vista, esa cara quedará de frente y el cubo en la posición canónica. Finalmente, el movimiento 2-1 completa el recorrido.
Esta era la axonometría más general, la llamada trimétrica, que se produce cuando los ángulos que forman las proyecciones de las tres aristas son todos diferentes. En este caso son también diferentes sus medidas aparentes ("escalas"). La arista perpendicular al lado más corto del triángulo es la de mayor escala, porque es la más frontal, dado que la cara perpendicular a ella es la que está más de canto, y corresponde al mayor ángulo entre ejes. El menor ángulo corresponde a la cara más frontal, al lado más largo del triángulo, y la arista perpendicular, por consiguiente, es la más de punta, con la escala menor.
A continuación se muestra el caso del triángulo isósceles, con dos ángulos entre aristas iguales y dos escalas también iguales (perspectiva dimétrica):
Finalmente, si los tres ángulos son iguales (120ª cada uno) el triángulo es equilátero y las tres escalas son iguales (perspectiva isométrica):
Cuando la dirección de proyección no es perpendicular al plano del cuadro tenemos la perspectiva oblicua. Es el caso de la dirección 3-4' que proyecta el cubo de la vista 3 en un plano, de canto en ella, que convenientemente girado de frente produce la vista 4':
Si en el caso anterior el plano de canto es paralelo a una cara, la proyección oblicua la conserva en su verdadera forma y magnitud. Entonces la llamamos perspectiva caballera o militar:
Si la proyección la efectuamos, no desde un punto infinitamente alejado (dirección 1-2) sino desde uno cercano V, y el plano de canto que servirá de cuadro lo hacemos coincidir con una cara, en la vista siguiente esta cara permanecerá en su verdadera magnitud, mientras la más próxima al punto de vista se agiganta pero conserva la forma. Las aristas paralelas a 1-2, en cambio coinciden en un punto de fuga V2: esta es la perspectiva cónica frontal.
Apoyando el cubo en una arista sobre el plano de canto, las cuatro paralelas a él conservan el paralelismo pero no la escala. Las otras aristas concurren en dos puntos de fuga situados en un horizonte. La alineación entre los vértices de esta proyección cónica oblicua con los correspondientes de la ortogonal y el punto V2 permiten situar cada punto en su lugar.
Ahora va el caso más general de la perspectiva aérea o de tres puntos de fuga. El cubo está colocado oblicuamente al plano de proyección. Las paralelas a las aristas trazadas por V definen un triedro trirrectángulo. triángulo de horizontes, y tres puntos de fuga.
Nuevamente la proyección ortogonal del punto de vista está alineada con las proyecciones de los vértices en las perspectivas ortogonal y cónica.
Aprovecharemos ahora lo aprendido para considerar, en cada uno de estos tipos de perspectiva, la representación de los ejes cartesianos, con sus puntos origen, unidad e impropio o del infinito. Partimos (vista 4) de tres ejes que formen entre sí ángulos distintos, siempre mayores de 90º y menores de 180ª (por ejemplo, 105º. 120º y 135º, que suman 360º). Todavía no conocemos las escalas respectivas.
En la vista 3 ponemos de canto el plano xy, con lo que queda de frente el eje z, que ya podemos devolver a la vista inicial. Esa será su unidad de medida en ella.
Pasamos a la vista 2. En ella xy estará de frente. Trazamos en ella las unidades correspondientes, que devolveremos a la vista 3 y luego a la 4. Ya tenemos las tres escalas.
El mismo procedimiento para los ejes de la perspectiva dimétrica:
Y para la isométrica, con ejes que forman entre sí ángulos iguales de 120º:
Una perspectiva oblicua arbitraria. Para obtenerla bastaría elegir tres ejes y tres escalas cualesquiera.
Claro que si queremos que tenga "buena pinta" habrá que recordar que a ángulos entre ejes más abiertos, planos más de canto, ejes perpendiculares a ellos más más de frente y escalas más próximas a la unidad. Inversamente, ejes con ángulos más próximos al recto, caras más frontales, ejes más de punta y escalas más próximas a cero. Teniendo estas cosas en cuenta las perspectivas serán más parecidas a la ortogonal.
Además los ángulos no deberían ser nunca menores de 90ª.
Y en la perspectiva caballera hay dos ejes perpenficulares, con escala real, y otro oblicuo, con escala que debería ser menor. Cuanto más pequeña mejor aspecto, pero si es minúscula se pierde la buena visión.
Perspectiva cónica frontal. Aparece un punto de fuga que permite obtener medidas proyectivamente sobre ese eje.
Perspectiva cónica oblicua. Dos puntos de fuga y el tercero en el infinito.
El caso más general, perspectiva aérea. Tres puntos de fuga. El triángulo de horizontes tiene lados paralelos al de trazas, y ambos deben ser acutángulos.
Con esto se ha establecido un método proyectivo general para situar puntos en toda clase de perspectivas, conocidas sus coordenadas, y así concluímos el capítulo cuarto.
No hay comentarios:
Publicar un comentario