La expresión gráfica en la ingeniería (1-a)

psicodiagnosticotv

Los fundamentos proyectivos de la representación

 

La historia de este libro vuelve a ser (¿cómo no?) la de una urgencia. Fue un curso en que cada fin de semana preparaba el material para las clases de la semana siguiente, a veces hasta altas horas de la noche del domingo. A mi lado, preparaba las suyas quien me acompaña desde hace tantos años (debo reconocer que mejor que yo a ella), codo con codo.

Debido a este origen apenas tiene texto, escrito en un gallego técnico de interpretación fácil para cualquier hispanohablante.

No estoy muy seguro de que el libro, tras mi marcha de la universidad, se haya seguido publicando y utilizando. Algún tiempo después de jubilarme seguía en la bibliografía recomendada, pero buscando ahora en internet no lo veo a la venta. La ficha bibliográfica existe, incluido el ISBN. El primer capítulo, en PDF, se puede descargar aquí.

Me he planteado si aportará algo traerlo al blog. Muchos de sus materiales repiten cosas ya lanzadas a estas anónimas olas hertzianas (espero que en algún caso se transformen también en ondas cerebrales), pero al ser posterior contenidos y notaciones son más sistemáticos. Hay aspectos, como el tratamiento guiado, fácil de usar, del sistema diédrico directo, que no he visto publicados. Por eso, y siendo lo último que completé sobre expresión gráfica, me decido a ponerlo a vuestra disposición.

Comienzo con un recordatorio del carácter lingüístico de la expresión gráfica, que me parece importante en estos tiempos ágrafos. Ni la escritura elaborada ni la imagen meditada son plato de consumo en la sociedad de la expresión en 140 caracteres y la imagen enlatada.

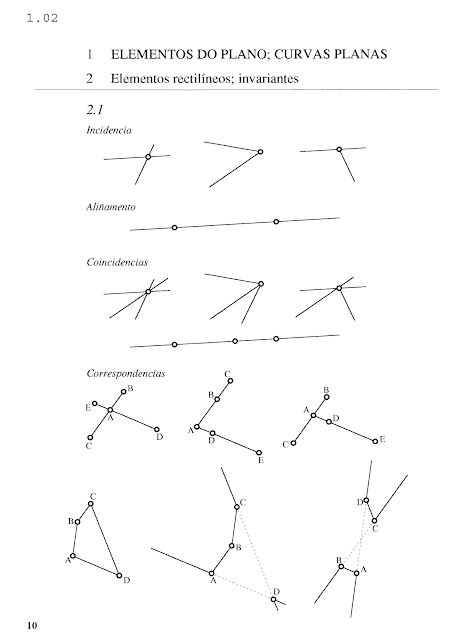
No es concebible la línea, base de la expresión, sin el punto y su movimiento. Analicemos éste:

Interacción de los puntos sobre la línea y de las líneas a través del punto. Cómo a través de diferentes formas particulares aparecen las mismas relaciones entre ellos. Con dos, tres y cuatro elementos:

De esos cuatro puntos, no alineados tres de ellos, surge una división del plano en partes. ¿Cuántas son realmente? Mirad bien los tres casos de incidencia que siguen y fijáos en las equivalencias y correspondencias entre puntos, líneas y áreas del plano que delimitan en cada figura:

Se puede establecer desde ahora que cinco puntos determinan el plano, y en él todos los demás elementos que contiene, con tal de que uno de ellos esté alineado con los otros dos pares. 

Los cuatro vértices definen siempre un cuadrilátero completo, con intersecciones entre sus lados en dos puntos más. La misma figura, cambiando la denominación de los puntos, representa planos diferentes que se corresponden entre sí. En todos hay tres cuadriláteros y cuatro triángulos, pero siempre algunos de ellos contienen un punto del infinito, porque para ir de un extremo al otro del mismo lado sin pasar por alguno de los demás puntos hay que marchar al infinito por una semirrecta y volver por otra de la misma recta:

Todos los cuadriláteros definen un plano que se puede hacer corresponder punto a punto con todos los demás. En estas figuras, cosas del pixelado de la imagen, apenas se ven las líneas diagonales de puntos que unen los vértices opuestos del cuadrado y las paralelas medias, que se corresponden con líneas de las otras figuras. Pueden trazarse considerando que tres líneas correspondientes que son paralelas en el cuadrado, en otros cuadriláteros lo siguen siendo, o bien se encuentran en algún punto común:

En los paralelogramos esas líneas son siempre paralelas:

El rombo no es más que un caso particular del anterior:

Otro caso, con el paralelogramo en otra posición:

En los trapecios algunas líneas conservan el paralelismo, que en otras se transforma en concurrencia. Aparece un horizonte que representa el infinito, y sobre él hallamos tres puntos de fuga. Un cuarto punto es el del infinito del horizonte, porque en el concurren las líneas paralelas:

En el trapezoide desaparece todo paralelismo en las líneas de la figura. El horizonte, ahora, contiene cuatro puntos de fuga:

Si en lugar de un cuadrado creamos una cuadrícula, podemos trazar otras líneas paralelas entre sí y comprobar la correspondencia con las representaciones perspectivas de la misma:

También tres puntos no alineados del plano pueden determinar representaciones perspectivas. Pero otra vez se necesita completar la terna con dos puntos más, de modo que uno de los cinco se alinee con los otros dos pares. 

Lo más simple es elegir dos puntos sobre sendos lados y unir cada uno con el vértice opuesto a él. Por la intersección de esas dos líneas, llamadas cevianas, se hace pasar otra ceviana desde el tercer vértice, que en el lado opuesto a él determina un sexto punto. Entonces queda definido el triángulo, que se puede hacer corresponder con uno equilátero, como antes el cuadrado con cualquier cuadrilátero.

Ahora los puntos de encuentro determinan un horizonte sobre el que hay seis puntos de fuga, tres para los lados y paralelas medias y otros tres para las alturas, hablando de todas estas líneas como perspectivas de un triángulo equilátero:

Puede construirse sobre esta base una malla triangular perspectiva:

Los cinco puntos que definen una perspectiva pueden situarse arbitrariamente sobre dos rectas, determinándola así en correspondencia con una malla cartesiana:

La malla cartesiana y su perspectiva:

Partimos de estos datos:

Proceso de construcción. ¿Podéis ver aquí un cuadrilátero completo?:

La construcción de los cuadriláteros unidad para las dos mallas:

Extendiendo las dos mallas:

Este proceso puede repetirse indefinidamente...

 ...y servir de base para dibujar figuras planas...

...y sus perspectivas:

Con esta sencilla mecánica establecemos las bases para la perspectiva en el plano.

(continúa, y finaliza, el capítulo primero)