Para ver la última publicación, pulsar aquí.
De dos maneras pueden interactuar dos piezas en contacto, el deslizamiento y la rodadura. En la entrega anterior se expusieron varios casos que utilizaban el movimiento helicoidal para deslizar un tornillo sobre la tuerca (o roscarlo en la madera, creando en ella la superficie sobre la que desliza), y otro caso que suponía desplazar una bola por el interior de un tubo helicoidal.
En la rodadura, en cambio, no debe haber deslizamiento recíproco. El principio de la rodadura, hacer coincidir distancias entre puntos de dos curvas de manera que se correspondan punto a punto sobre una tangente común, se vio al estudiar las curvas denominadas evolventes y evolutas, pero sin salir del plano. Vamos a presentar ahora mecanismos que llevan la rodadura al espacio, produciendo un giro de eje no paralelo al causante, a partir también del movimiento helicoidal.
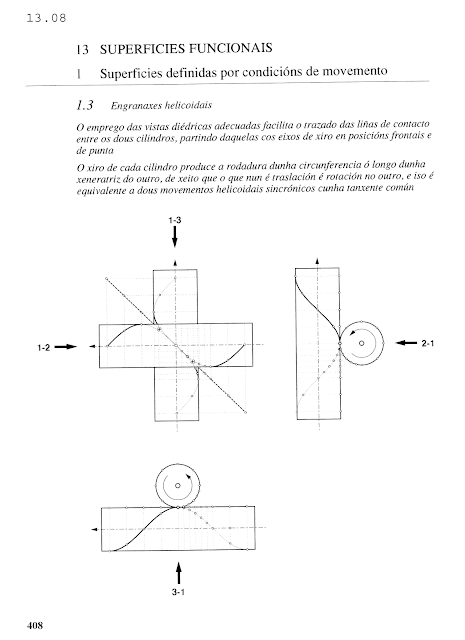
Lo que queremos lograr se ve en el dibujo final de la página que sigue: ¿cómo hacer que el giro de un cilindro produzca el del otro?
Vemos aquí los puntos sucesivos de contacto sobre uno y otro cilindro obtenidos mediante giros de 15º.
Como mecanismo de agarre que impida el deslizamiento podemos grabar en los cilindros otras hélices ortogonalmente dispuestas, que tengan como perfiles los dientes de un engranaje plano, desplazados sobre ellas.
En la vista 4 de la figura siguiente se visualiza el plano en que se produce la rodadura entre dos puntos en contacto. En esta vista coinciden las dos hélices, y la curvatura adecuada permite diseñar el perfil del diente, como una evolvente de cada línea en contacto.
El diseño del diente se realiza como en los mecanismos planos, haciendo coincidir los radios de curvatura de la hélice, de la elipse que es sección del cilindro y de la circunferencia osculatriz de ambas, y a partir de ahí la evolvente de esta circunferencia nos da el perfil del diente necesario.
(Los dientes cuyo perfil represento son evolventes de circunferencia, que en este caso es la osculatriz de la curva helicoidal y de la elipse sección del cilindro. Al final de esta entrega añado un recordatorio del concepto de evolvente, que apareció fugazmente aquí, en la página 38 del libro, ilustración 1.30).
Con este procedimiento general de obtención del engranaje helicoidal no es necesario que los cilindros sean iguales ni sus ejes perpendiculares. Desde luego, cuando los diámetros no sean iguales habrá que adaptar el perfil de los dientes para los dos cilindros, y la razón entre el número de dientes de ambos ha de coincidir con la de los radios de los cilindros (el cilindro mayor tendrá más dientes, en la misma proporción).
En el punto de contacto, las dos hélices tendrán una tangente común. y en el movimiento se conservarán las distancias entre puntos, tanto para ella como para ambas curvas.
Como anexo al tema, se incluyó una alusión a las superficies dadas por funciones, como esta de un paraboloide reglado, en la que a cada punto del plano XY corresponde una cota Z:
Y otro caso, en que los valores de X, Y, Z dependen de parámetros. En este se combinan tres movimientos con características distintas en las tres direcciones principales del espacio. La superficie definida depende de su combinación. Son infinitas las que se pueden obtener, para aplicaciones mecánicas o simplemente para el diseño con intenciones estéticas.
La medida de distancias sobre una curva se materializa muy bien enrollando y desenrolando un hilo inextensible sobre ella.
Cada posición del hilo es una tangente, y cada punto del hilo describe una evolvente de la curva. Las perpendiculares por cada punto son a su vez tangentes a otra curva, que se llama evoluta. Es fácil ver que la evolvente de la evoluta es la curva inicial:
Esta correspondencia recíproca entre evolvente y evoluta es la que hace que cuando en un engranaje una pieza rueda sin deslizarse sobre otra también lo hacen los dientes en contacto, cuyo perfil es de evolvente de la curva correspondiente, lo que minimiza la fricción.
Poco queda ya para el final del libro, pero todavía...











Muy interesante. Como siempre.
ResponderEliminar