Perspectiva unificada V

Capítulo III

Proyección de planos

Si el plano es sólo un continente vacío, proyectar un plano sobre otro no tiene mucho sentido. Lo adquiere únicamente cuando proyectamos el contenido.

La sombra invisible del hombre invisible no daría información alguna sobre él

De esa "proyección de contenidos" voy a tratar en el capítulo tercero del libro que vengo comentando desde aquí hasta llegar, por ahora, aquí. En este último lugar proyectar una recta obteniendo otra sólo tenía sentido si se establecía biunívocamente la relación entre los puntos de ambas, relación que ahora hemos de establecer entre los puntos y rectas de figuras más complejas, manteniendo, además las relaciones internas entre los elementos en cada uno de los planos imagen y objeto.

Antes de continuar, debo aclarar que gran parte de la finalidad de esta publicación, lo que más me ha movido a ella, es independizar los trazados, en la medida de lo posible, del corsé de los "sistemas de representación", trabajando directamente sobre el plano de proyección.

Esto puede hacerse de dos formas.

La primera, ya apuntada, es imaginar el espacio contiguo al plano del dibujo, situando en él tanto los objetos a proyectar como el centro de proyección. Y en caso de proyecciones desde puntos muy remotos (paralelas), la dirección correspondiente.

Pero cuando los objetos son planos, y este es el caso de que me ocuparé ahora, puede trabajarse directamente con ellos en el plano del espacio proyectado sobre el del dibujo, aprovechando los invariantes proyectivos, y en particular la cuaterna armónica. Aunque en ciertos casos también la proporción (razón simple) y la medida.

Veamos, para comenzar, cómo se proyectan dos paralelas, que definen ya un plano, desde un punto V. Proyectaremos en cada una de ellas un segmento dado por dos puntos O,U, a los que añadiremos su punto medio M y el del infinito I, obtenido mediante un rayo paralelo a ambas. Todos los puntos, incluído el impropio común a las tres rectas, tienen una imagen distinta del punto objeto, excepto los de intersección con el plano de proyección (trazas). Desde luego, se mantienen las cuaternas armónicas (MIOU) entre los extremos de cada segmento, los puntos medios y el punto impropio.

Los dos puntos cuya imagen coincide con ellos mismos definen la traza del plano proyectado, recta común a los dos planos:

De la misma manera podemos proyectar dos rectas que se cortan, definiendo un plano, y las correspondientes cuaternas armónicas que forman en ellas y sus imágenes la intersección O y los puntos unidad U, medio M e infinito I:

Esta es la proyección de un triángulo equilátero. Buscad las cuaternas armónicas en el objeto y su imagen:

Y esta la de un cuadrado. Trece puntos de mucho interés forman hasta once cuaternas, su centro, los cuatro centros de sus lados, los cuatro vértices y los cuatro puntos del infinito de lados y diagonales:

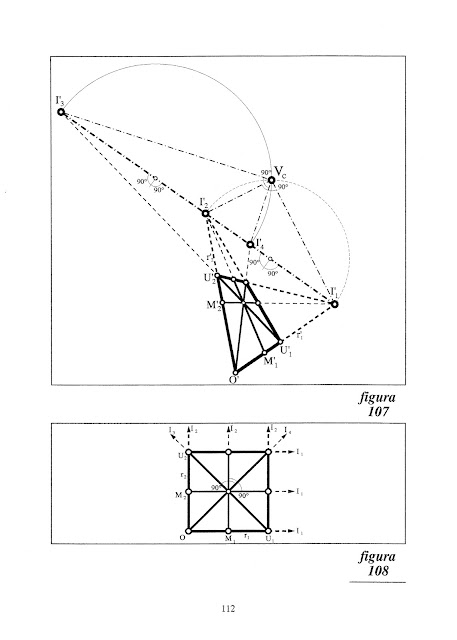
También el triángulo y su imagen proporcionan cuaternas armónicas. Compárense la imagen con el triángulo equilátero, en el que los puntos "medios" lo son realmente, y también son tales los del "infinito".

La comparación de las figuras que siguen sugiere (y así es) que todo triángulo puede ser la perspectiva de otro cualquiera, Y que todos se pueden corresponder proyectivamente, así como sus cevianas, que son las líneas que unen los vértices con cualquier otro punto del plano, y de las que son casos particulares las mediatrices, bisectrices, alturas y medianas.

La proyectividad entre cuadriláteros es algo más restringida y unívoca. Ya no es suficiente elegir un punto cualquiera y unirlo con los vértices para buscar correspondencias, porque necesariamente han de establecerse como referencia las intersecciones de diagonales. Pero todos los cuadriláteros son perspectivos, y todos pueden ser la perspectiva de un cuadrado.

Compruébese que en V, que podemos llevar al espacio girándolo sobre la recta del infinito de la imagen, concurren cuatro rayos proyectantes que forman entre sí ángulos de 45º, los mismos que forman lados y diagonales de un cuadrado, único cuadrilátero en que esto ocurre.

Así que el cuadrilátero puede ser imagen de un cuadrado sito en un plano paralelo al que formen V y el horizonte.

Un mismo triángulo es incluso perspectivo consigo mismo, como los de las figuras que siguen, sin más que definir sobre él distintas cevianas:

Cosa que no ocurre con los cuadriláteros. Todos pueden ser perspectivos unos con otros, pero la perspectiva de cada uno es única, así que si coinciden los perímetros coinciden todos los puntos, lo que no le pasa a los triángulos.

Un cuadrado y un hexágono y dos perspectivas (paralela en un caso, central en el otro):

Malla triangular y su perspectiva:

Malla cuadrada y perspectiva de la misma:

En una malla cuadrada pueden inscribirse circunferencias. La circunferencia puede ajustarse a otras mallas, siempre cuadradas, que en realidad son la misma sometida a un giro. Pero una elipse, que puede inscribirse en diferentes paralelogramos, puede definir con ellos diferentes mallas. Una sola de ellas es rectangular, con líneas paralelas a los ejes de la elipse. Las demás son romboidales, definiendo siempre las paralelas medias de estos romboides un par de diámetros conjugados.

Las mallas pueden tomarse como base para manejar diferentes direcciones, que en las perspectivas confluyen en otros puntos límites sobre el horizonte.

De todos los puntos límite nos interesan sobre todo los que corresponden a las cuatro direcciones del plano cartesiano que definen los lados y diagonales de un cuadrado (en términos cartográficos serían N, NE, E, SE, S, SO, O y NO). A continuación, una manera de definirlas.

Dos circunferencias ortogonales entre sí, con centros en el horizonte, que se corten en el punto de vista (y es indiferente que éste se halle en el plano que proyecta el horizonte o que haya sido abatido, girando sobre él, hasta el plano de proyección) definen sobre el dicho horizonte cuatro puntos que, no sólo forman la cuaterna, sino que son los puntos límite de lados y diagonales de un cuadrado. Cualquiera otra dirección del plano halla también definido su punto límite:

Si en un cuadrado había trece puntos notables (cuatro de ellos impropios) en su imagen proyectada podemos determinarlos con toda precisión a partir del perímetro cuadrangular. Si en esa imagen perimetral no hay dos lados paralelos entre sí ni al horizonte, aquellos cuatro puntos impropios serán cuatro puntos de fuga que sobre el horizonte formen otra cuaterna armónica.

El cuadrilátero es la figura determinante en la proyectividad, porque siempre es una imagen única de un cuadrado.

En la figura 129, las proyecciones paralelas desde I y desde J sobre una recta por H nos proporcionan dos escalas para medir sobre los lados correspondiente del cuadrado y sobre toda malla basada en él. La proyección desde M nos permite en cambio definir los puntos límite sobre un horizonte cualquiera.

La figura 130 se corresponde punto por punto con la anterior en una perspectiva. También ahora la recta por H nos da escalas de medida, al ser paralela al horizonte definido por los puntos límite I, J, K, L.

En la figura 131 hemos girado sobre la recta por H los lados del cuadrado. Si ahora buscamos las direcciones de las proyecciones paralelas, tendremos los puntos impropios D desde los que proyectar los lados del cuadrado y las rectas de su malla correspondiente utilizando la escala verdadera.

Esto es lo que hemos hecho correlativamente en la figura 132. Los puntos D, ahora puntos propios sobre el horizonte (puntos de distancia), miden en su verdadera magnitud sobre la recta las distancias en las direcciones de los lados.

Y para obtenerlos ha bastado utilizar la construcción de la figura 126, girando ahora desde los puntos I y J las distancias desde ambos a V. Puede comprobarse que arcos y ángulos son aquí iguales a los de los giros por H de la figura anterior.

Hemos visto que el cuadrado es la figura inequívoca para trazar figuras que pueden ser imágenes de las de un plano cartesiano. En el caso del triángulo no basta definir su perímetro, sino que hay que dar dos puntos más sobre sus lados que puedan equivaler a sus puntos medios (el centro del tercer lado queda fijado por la tercera ceviana, que ha de pasar por la intersección de las otras dos). En estas condiciones podemos definir la imagen proyectiva de una malla triangular equilátera. Lo comprobamos en la figura 133.

Podemos preguntarnos si cualquier otro polígono de cinco o más lados pueden definir una proyectividad entre planos. La respuesta es no: el pentágono y el hexágono de la figura 134 no puede corresponderse en todos los puntos que definen con los de la figura 135. Basta este contraejemplo para negar esa hipótesis. La correspondencia entre los centros ha quedado destruida.

Pero eso no imposibilita la obtención de perspectivas de tales polígonos desde la propia correspondencia proyectiva. A continuación dejo la construcción de la imagen de un pentágono regular. La clave para obtenerla es en primer lugar fijar en el plano imagen, a semejanza de lo hecho para el triángulo (allí eran dos lados y dos "puntos medios"), cinco puntos (ahora tres lados y el "punto medio" de uno de ellos) y seguir por el orden indicado las operaciones en las dos figuras. Los paralelismos de la figura cartesiana se convierten en concurrencias en la proyectada.

Para vencer una dificultad inicial, fijaos en que se comienza tratando en ambas figuras el cuadrilátero 1,2,3,4 como perspectiva de un cuadrado.

En todos los casos, cinco puntos ligados por una relación defnen la perspectiva (en el triángulo eran tres vértices arbitrarios y dos puntos sobre ellos, en el pentágono han sido cuatro vértices arbitrarios y un punto que ya no lo era totalmente). Pues bien mirado, eso mismo ocurría para el cuadrado, porque lo definen cuatro puntos arbitrarios (vértices) y el bien definido "centro" como intersección de las diagonales.

¡Curiosidades proyectivas, que permiten trabajar comparando planos objeto e imagen sin realizar la proyección en el espacio!

Uff... tal vez un poco denso, pero espero haber sido, al menos, sintético.

(sigue)