Capítulo I
Proyección de cuerpos punto a punto
La imagen que sigue a este exordio-incordio expresa muy bien lo que es una proyección. En el caso de las sombras lo que se proyecta es un "contorno aparente", una línea trazada sobre el objeto que separa lo que "se ve" de lo que "no se ve". ¿Y quién ve?
Aunque el fenómeno físico esté invertido, la geometría del fenómeno es idéntica para el rayo luminoso que "va" hacia el objeto desde una fuente de luz y para el que "viene" del objeto iluminado hasta un ojo que lo percibe.
Esta identidad constructiva es aprovechada en la computación gráfica por la técnica de trazado de rayos (ray tracing).
De manera que podemos imaginar el foco luminoso como un ojo que "ve" lo que ilumina. De hecho los antiguos pensaban que los rayos visuales partían del ojo hacia los objetos, en vez de recorrer el camino inverso.
Así que el sol "ve", mediante una proyección paralela, la superficie del suelo que iluminan sus rayos, y deja de ver la superficie en sombra, que sustituye por la imagen del niño y la de la farola.
Esta proyección es oblicua. Si el sol estuviera en el cenit sería ortiogonal.
Y cuando anochezca y el niño salte bajo a luz de la farola producirá una proyección central.
El sencillo principio geométrico de la proyección lo hemos visto en la entrega anterior de esta serie que comenzó aquí.
El primer capítulo, cuyas figuras comento a continuación, y que podéis descargar aquí, pretende enseñaros un método sencillo e intuitivo para realizar estas tres únicas proyecciones.
La idea es relacionar el plano de la representación con su entorno espacial inmediato, en el que situaremos puntos y los rayos que los proyectan sobre él.
A continuación, después de haber comprendido cómo se efectúa la proyección en el espacio, aprenderemos a llevarla a cabo sobre el plano mismo, mediante la operación de "abatir" sobre él otro plano de ese espacio inmediato en que hemos realizado la proyección.
Para materializar del modo más palpable esta idea tomaremos como plano de proyección el de una lámina de dibujo:
La esquina de la lámina nos servirá como origen para las dos coordenadas del plano, y a ellas añadiremos una tercera, perpendicular a él, que servirá para situar puntos del espacio inmediato:
Así, para localizar el punto A utilizaremos, además de las coordenadas x e y del plano, la tercera coordenada z, que en este caso lo van a localizar cuarenta milímetros por encima de la lámina. Y pondremos esta cifra (llamémosla cota) entre paréntesis a continuación de la proyección ortogonal del punto del espacio sobre el plano:
Podemos añadir un segundo punto B no coincidente con el primero y aún un tercero C no alineado con ellos, ambos puntos dados por sus proyecciones, que los sitúan en el plano, y por sus cotas, que los elevan sobre él. Tendremos respectivamente un segmento y un triángulo en la lámina, como proyecciones ortogonales de unos elementos del espacio situados por encima de ellas:
Añadir un cuarto punto D, no coplanario con los otros tres, no cambia el procedimiento. Pero ahora hay una diferencia notable con lo anterior, porque mientras los cuatro puntos del espacio definen un sólido, que es tridimensional, en el plano son representados por una figura de dos dimensiones.
Es fácil imaginar, viendo la figura proyectada, la posición de los puntos del espacio, con sólo elevar los puntos proyectados hasta la altura indicada por su cota.
Consideremos el rayo que proyecta uno cualquiera de estos puntos, o un punto genérico P, sobre el plano. Se trata de una recta perpendicular a él, y perpendicular será también cualquier plano que la contenga. Ese plano cortará al del dibujo en una traza, y si lo giramos sobre ella hasta que coincida con la lámina, el rayo así caído será, naturalmente, perpendicular a dicha traza.
El punto del espacio quedará abatido sobre el plano. Al repetir la operación con los infinitos planos que contienen al rayo se obtiene la circunferencia que definen todos los abatimientos posibles del punto, cuyo radio será la cota del mismo. La llamaremos circunferencia de distancia:
Pero mientras las perpendiculares a la lámina tienen todas una única dirección, para las oblicuas hay infinitas direcciones, las cuales, como dependen de dos variables (la inclinación y el plano vertical que las contiene) son en número doblemente infinitas.
Comparemos la dirección ortogonal con una oblicua cualquiera dada por un vector v, que definiremos mediante dos puntos cualesquiera que arbitrariamente serán origen y extremo. Vamos a comparar ese vector con el ortogonal al plano del dibujo.
Lo primero que observamos es que el vector está contenido en un plano ortogonal. Aplicando ambos vectores al punto A se los ve dentro de un plano paralelo al anterior.
Si giramos ambos planos paralelos simultáneamente sobre sus trazas respectivas, conservando el paralelismo en todo momento, al llegar a confundirse ambos en el plano de la lámina habremos realizado en éste la operación imaginada en el espacio. El resultado será la doble imagen proyectada del punto, y aparecerá, además de la proyección ortogonal, la proyección oblicua según la dirección del vector dado.
Esto es lo que habremos dibujado, a partir de las tres coordenadas del punto y las tres del vector, porque uno de sus extremos puede ser un punto cualquiera, desde el que las aplicaremos para obtener el otro.
(Aunque las coordenadas sean tres, las variables son dos, porque la primera puede ser siempre una unidad fija).
Se puede aplicar el procedimiento a cualquier número de puntos con los que definamos un objeto en el espacio. Con dos puntos proyectaremos un segmento:
La operación imaginada en el espacio la realizaremos así en el plano:
Tres puntos, vértices de un triangulo, y sus proyecciones ortogonal y oblicua:
Todo hecho sin salir de la lámina:
La operación del espacio trasladada al plano para los cuatro vértices de un tetraedro:
Los trazados, sobre la lámina. Observemos que la arista DB, que es vista para la proyección ortogonal, aparece oculta en la oblicua. El contorno aparente es en el primer caso el triángulo BCD, y en el segundo el cuadrilátero ABCD.
Con el cambio del punto de vista se altera el contorno aparente, y con ello las partes vistas y ocultas del objeto. Vemos esto todos los días en las cambiantes fachadas de un edificio que va iluminando el sol en su recorrido.
Y otra observación: si una sola proyección ortogonal no define inequívocamente el objeto en el espacio, al introducir otra, necesariamente oblicua, el sólido queda perfectamente identificado, así como su posición.
Podemos imaginar los dos ojos infinitamente lejanos de un dios (uno de ellos necesariamente bizco) que "crean" el objeto en el espacio.
Dejemos en paz a la Divinidad y acerquemos un ojo humano al papel. El conjunto de todos los abatimientos posibles del ojo, conservando la distancia a su proyección ortogonal, nos define una circunferencia de distancia del punto de vista:
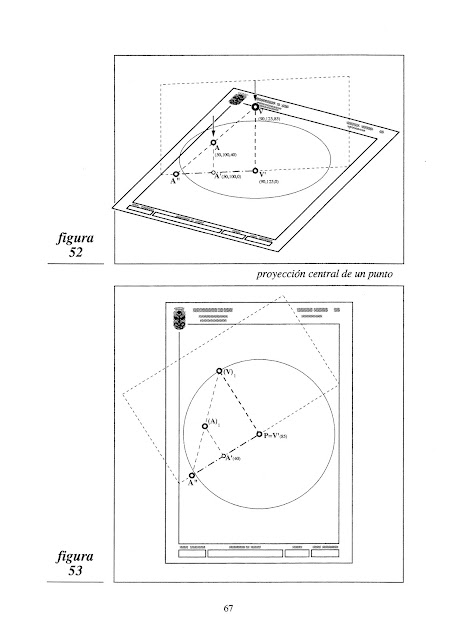
Al proyectar ortogonalmente el punto A y el punto de vista V, los rayos proyectantes de ambos definen un plano. Abatámoslo como ya sabemos y podremos obtener la proyección central de A:
Los puntos abatidos (V) y (A) y los proyectados P=V' y A' definen, alineado con ambos pares, el punto V'', que es la proyección central buscada. El ojo V no sabría distinguir el objeto de su imagen:
El procedimieno puede repetirse para el par AB, pero para cada punto hay que hacer un abatimiento distinto:
Esta es la construcción que nos deja ver a un tiempo la proyección paralela ortogonal y la central. Podemos situar el segmento en el espacio, pero para "verlo" en relieve ¡habría que tener un ojo en V y el otro infinitamente lejos, en la dirección perpendicular al papel!
Idéntica construcción para proyectar un triángulo:
Las dos proyecciones sobre el papel, con tres abatimientos, uno por vértice:
Y lo mismo para el tetraedro:
Con cuatro abatimientos. Fijaos como ahora, como en la proyección oblicua, cambian el contorno aparente y las partes vistas y ocultas:
Para finalizar, dejo aquí un esquema de todos los casos posibles de proyecciones, ortogonal, oblicua y central, y de las dos posibilidades de posicionamiento de un elemento rectilíneo en relación con el plano de proyección, que no puede ser sino paralelo al plano u oblicuo respecto a él.
Las dos proyecciones paralelas reproducen la forma y magnitud del objeto cuando es paralelo al plano, pero cambian la escala, conservando las proyecciones tan solo las razones simples (proporciones, para entendernos), si la recta que proyectamos es oblicua. En el caso de la ortogonal hay una reducción de la escala, pero en la oblicua puede haber reducción o aumento, y aún igualdad, como puede comprobar cualquiera observando a lo largo del día cómo se encoge o se estira la sombra de un poste con el movimiento del sol.
La proyección central nunca conserva la medida, pero mantiene las proporciones cuando el objeto es paralelo al plano. Si la recta incide oblicuamente en él no se conserva ninguna de las dos cosas, aunque sí la proporción de proporciones llamada razón doble, y concretamente la cuaterna armónica, que relaciona proyectivamente entre sí los puntos origen, extremo, medio e infinito de un segmento.
Con estos simples materiales trabaja cualquiera de los sistemas de representación. Conocerlos nos ahorrará mucho aprendizaje lento y poco útil.
Aunque claro, como ahora dibujan las máquinas, basta con que sepan estas cosas los programadores que las instruyen. El espeso vulgo es mejor que no sepa la razón (simple, ¡hay que ver!) de muchas cosas.
Igual ocurre con todos los eficientes mecanismos de nuestra cultura dominante. Lamentemos juntos la creciente especialización que deja siempre las grandes decisiones en manos de "expertos".























No hay comentarios:
Publicar un comentario