Esquemas sinópticos
descarga esquemas tomo IIntroducción
descarga archivoÁngulos poliedros
descarga archivoRedes planas
descarga archivoFormas abovedadas
descarga archivoCompartimentación superficial del plano y la esfera
descarga archivoPoliedros regulares duales y romboedros
descarga archivoAñado este nuevo este enlace al archivo en que me ocupo de los poliedros semirregulares.
Los poliedros semirregulares (llamados sólidos arquimédicos para distinguirlos de los regulares o sólidos platónicos), tienen todos los vértices idénticos y sus aristas son iguales, pero sus caras no tiene todas el mismo número de lados.
Empleando la notación de Schläfli, en la que las cifras entre paréntesis indican el número de lados de los polígonos que consecutivamente encontramos en cada vértice, los poliedros que siguen son, por el orden de la fotografía, cubo achatado (3,3,3,3,4), gran rombicuboctaedro (4,6,8), rombicuboctaedro (3,4,4,4), octaedro truncado (4,6,6), cuboctaedro (3,4,3,4) y cubo truncado (3,8,8). Los acompaña el poliedro regular básico, el cubo (4,4,4), y falta a la cita su dual, el octaedro (3,3,3,3).
En estos modelos los tamaños son muy diferentes por haberlos construido con aristas de igual longitud; pero con tamaños adecuados todos podrían inscribirse en un mismo cubo, como tendremos ocasión de comprobar.
Constituyen la familia del cubo, y se caracterizan por compartir los mismos elementos de simetría, con excepción del primero, carente de simetría bilateral, pero que la posee cíclica. Es decir, en un espejo su imagen se ve claramente invertida, pero puede coincidir consigo mismo girando alrededor de un eje.
En la familia del dodecaedro, los poliedros correspondientes son: dodecaedro achatado (3,3,3,3,5), gran rombiicosidodecaedro (4,6,10), rombiicosidodecaedro (3,4,5,4), icosaedro truncado (5,6,6), icosidodecaedro (3,5,3,5) y dodecaedro truncado (3,10,10). Completa la serie el poliedro regular básico, el dodecaedro (5,5,5). Falta en la imagen su dual, el icosaedro (3,3,3,3,3).
El sistema del tetraedro es peculiar, porque muchos de sus miembros "se escapan" al sistema del cubo, mientras otros coinciden en distintos casos.
Comprobémoslo.
De los polígonos que han aparecido en estos dos casos, hay uno determinante del sistema. Para el cubo es el cuadrado y para el dodecaedro el pentágono. Llamaré x a ese polígono y generalizando, obtendremos, a partir de las diferentes fórmulas de Schläfli. Pido perdón a los expertos por una nomenclatura engorrosa que me inventé sin contrastarla con nadie. Por poliedro hay que entender el básico en la primera posición del término y el dual en la segunda.
"poliedro achatado" (3,3,3,3,x), "gran rombipolipoliedro" (4,6,2x), "rombipolipoliedro" (3,4,x,4), poliedro truncado (x,6,6), "polipoliedro" (3,x,3,x) y nuevamente poliedro truncado (3,2x,2x).
Si el polígono clave era en los casos anteriores el cuadrado en un caso y en el otro el pentágono, para el tetraedro ha de ser necesariamente el triángulo.
Los poliedros resultantes de la comparación con los casos anteriores serían: "tetraedro achatado" (3,3,3,3,3), "gran rombitetratetraedro" (4,6,6), "rombitetratetraedro" (3,4,3,4), tetraedro truncado (3,6,6), "tetratetraedro" (3,3,3,3) y tetraedro truncado (3,6,6).
Fórmulas generales:
(3,3,3,3,x) (4,6,2x) (3,4,x,4) (x,6,6) (3,x,3,x) (3,2x,2x)
Sistema del cubo (x=4):
(3,3,3,3,4) (4,6, 8) (3,4,4,4) (4,6,6) (3,4,3,4) (3, 8, 8)
Sistema del dodecaedro (x=5):
(3,3,3,3,5) (4,6,10) (3,4,5,4) (5,6,6) (3,5,3,5) (3,10,10)
Sistema del tetraedro (x=3):
(3,3,3,3,3) (4,6, 6) (3,4,3,4) (3,6,6) (3,3,3,3) (3, 6, 6)
Aquí comienzan las simplificaciones y las fugas. Como el tetraedro tiene por figura dual otro tetraedro, encontramos en dos lugares al tetraedro truncado (3,6,6). En cuanto a las fugas, El "gran rombitetratetraedro" (4,6,6) huye al sistema del cubo, pues resulta ser un octaedro truncado. También escapan el "rombitetratetraedro" (3,4,3,4), que es un cuboctaedro, y el tetratetraedro (3,3,3,3), que es el octaedro.
Queda como único miembro exclusivo del grupo el tetraedro truncado (3,6,6).
No son estos los únicos sistemas de simetría, ni los únicos poliedros semirregulares. pero sí son los sistemas isótropos en el espacio, porque estos poliedros y sus posibles redes no tienen una única dirección privilegiada.
Existen otros sistemas anisótropos en el espacio, con una sola dirección privilegiada. Sus poliedros y acoplamientos no tienen las mismas propiedades en cualquier dirección. Son los prismas, de fórmula (4,4,x), y los antiprismas (3,3,3,x). En ambos casos x puede tomar cualquier valor mayor que 2, y en los dos se trata, evidentemente, de poliedros semirregulares. Pero de nuevo hay excepciones: el prisma cuadrangular (4,4,4) es un cubo, y el antiprisma triangular (3,3,3,3), un octaedro.
Los poliedros semirregulares isótropos que resultan de la intersección del básico y su dual, que con tamaños variables comparten los mismos elementos de simetría, son los poliedros truncados y los "polipoliedros". Dejo aquí un ejemplo, en el sistema del cubo, en que octaedros de distintos tamaños se cortan con un cubo (4,4,4) y producen, sucesivamente: cubo truncado (3,8,8), cuboctaedro (3,4,3,4), y octaedro truncado (4,6,6). Se ha completado la figura con otros dos octaedros (3,3,3,3), ya totalmente interiores al cubo, que intervienen en redes poliédricas que llenan el espacio.
Para el sistema dodecaédrico tenemos una figura semejante. Icosaedros que cortan a un dodecaedro (5,5,5) y producen en su interior dodecaedro truncado (3,10,10), icosidodecaedro (3,5,3,5), y octaedro truncado (5,6,6). Por último, el octaedro dual (3,3,3,3,3) que tiene sus vértices en los centros de las caras del dodecaedro.
Y también el tetraedro (3,3,3), seccionado por las caras de poliedros duales que también son tetraedros, lleva en su seno otros poliedros, que son sucesivamente tetraedro truncado (3,6,6), octaedro (3,3,3,3), y otro tetraedro truncado (3,6,6), en posición dual. Finalmente el tetraedro dual (3,3,3) con vértices en los centros de las caras del básico. Como queda dicho, solamente el truncado es a la vez semirregular y específico del sistema.
Pero en las fotografías podemos contar hasta trece poliedros después de suprimir los tres básicos que figuraban en ellas. Y en estos últimos dibujos solo han aparecido siete inscritos en los básicos, mas dos intrusos, uno sin derecho a voto y otro que quería votar dos veces:
CT (3, 8, 8) CO (3,4,3,4) OT
(4, 6, 6)
DT (3,10,10) ID
(3,5,3,5) IT (5, 6, 6)
TT (3, 6, 6) O (3,3,3,3) TT
(3, 6, 6)
No son nueve, sino siete, porque el octaedro es regular y el tetraedro truncado se repite.
Vamos a localizar a los seis cuerpos que faltan.
En primer lugar, si hubiera dos poliedros en cada sistema con tres tipos de caras ya habrían aparecido los seis. Veamos que no es así. Porque sólo obtenemos tres nuevos. Las iniciales corresponden a “gran rombipolipoliedro” (GRPP) y “rombipolipoliedro” (RPP):
GRPP (4,6,2x) RPP (3,4,x,4)
GRCO (4,6, 8) RCO (3,4,4,4)
GRID (4,6,10) RID (3,4,5,4)
Se han tachado, porque no tienen caras de tres clases, poliedros que ya habían aparecido. Uno de ellos, el rombicuboctaedro (3,4,4,4), aunque no cumple el requisito de las tres clases de caras, sí precisa de la intervención del romboedro del sistema, pero no así los otros dos. Hay entonces cuatro genuinos "rombopoliedros". Pero todos los del listado se obtienen de la misma forma: de las intersecciones de los poliedros básico y dual de cada sistema, añadiendo a las mismas los romboedros correspondientes, que son respectivamente rombododecaedro, rombotriacontaedro y cubo, considerado éste como rombohexaedro.
Así como duermen las notas en las cuerdas del arpa y dentro de la piedra estaban ya desde una eternidad las esculturas de Miguel Ángel, estos poliedros surgen del interior de los romboedros si encargamos de eliminar lo que sobraba a los poliedros básico y dual. Aunque suene prosaico después de estas imágenes poéticas, os invito a extraerlos del interior de una patata.
Recortando los vértices del rombododecaedro con las caras del cubo (4,4,4) y las del octaedro (3,3,3,3) aparece el rombicuboctaedro (3,4,4,4):
Y si recortamos nuevamente con un cubo y un octaedro de menor tamaño, tendremos el gran rombicuboctaedro (4,6,8):
No tan fácilmente vemos lo que ocurre en el sistema del dodecaedro, pero si os fijáis bien en los cortes dados en las caras rómbicas, veréis cómo de un recorte semejante de los vértices de cinco rombos con un dodecaedro (5,5,5) y los de tres rombos con un icosaedro (3,3,3,3,3), aparece este rombiicosidodecaedro (3,4,5,4):
Un corte más profundo, con poliedros de menor tamaño, extrae el gran rombiicosidodecaedro (4,6,10):
Del poliedro básico y del dual también pueden extraerse estos poliedros.
Para el tetraedro habría que recortarle las aristas con su rombohexaedro, que es un cubo, y los vértices con un tetraedro en posición dual. Hay que situar las seis caras del cubo paralelamente a las aristas del tetraedro.
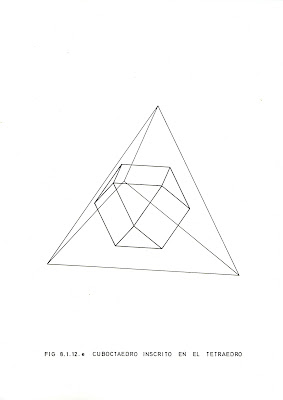
Así obtenemos un octaedro truncado (4,6,6), que tal resulta ser el "rombitetratetraedro", y, con cortes más profundos, el cuboctaedro (3,4,3,4), o "gran rombitetratetraedro":
De todos ellos se ha destacado un gajo, que es un módulo (un veinticuatroavo del volumen total) con doce de los cuales ("de la mano derecha" y otros doce simétricos ("de la mano izquierda") se puede componer la figura entera.
Este es el cuboctaedro, y podemos comprobar que cuatro de sus caras triangulares son aún las del tetraedro de partida:
Y este el octaedro truncado; cuatro caras hexagonales pertenecen al poliedro básico.
Aquí comprobamos que los dos poliedros podrán haberse obtenido también a partir de un cubo:
Lo dejo aquí por hoy. Planteo ahora otras dos cuestiones, que abordaré en otro momento, que tal vez se hayan planteado también quienes hayan sentido curiosidad por este tema:
¿Cuáles son los misteriosos cuerpos ("poliedros achatantes") que eliminan de los poliedros básicos de cada sistema "lo que sobraba" para obtener los extraños "poliedros achatados"?
¿Puede extenderse el estudio a los sistemas planos de simetría construidos sobre el triángulo equilátero y el cuadrado?
(sigue)
(sigue)













No hay comentarios:
Publicar un comentario