Una tesis geométrica. División pentagonal del espacio (II)

Si habéis montado los romboedros cuyo recortable dejé aquí, si también construisteis los triedros en los que alojarlos, si habéis probado a arracimar esos alojamientos, y en particular a lograr que compongan así un cerramiento completo de todo el espacio alrededor de un vértice, estaréis en las mejores condiciones para interpretar lo que sigue.

Se comprenderá mejor aún si los triedros se han fabricado sobre su versión con sectores circulares, pues entonces al agruparlos completarán una esfera, a la manera de esos farolillos de papel que se cuelgan en los cumpleaños infantiles. o como una versión movidilla y esférica de los panales de abejas.

Como hicimos en este lugar, partimos del pentágono para construir con su módulo un rombo y agrupamos cinco de estos rombos para formar una estrella. Ángulos del rombo, 72º y 108º.

También un decágono regular nos sirvió para construir con su módulo una estrella de 10 puntas, con diez rombos de ángulos 36º y 144º.

La simetría de estas dos figuras planas, que se pueden combinar de infinitas formas para formar un mosaico sin fin, induce a buscar algo semejante en el espacio. En un icosaedro, consideremos el triedro con vértice en su centro O y aristas V_i, V_j, V_k. V_i y V_j son vértices contiguos, mientras V_k no es contiguo ni opuesto a ninguno de ellos. Obsérvese que estas tres posiciones relativas (contiguos, opuestos o ninguna de ambas cosas) son las únicas posibles entre los vértices del icosaedro.

Situando en el extremo de cada arista segmentos iguales y paralelos a las otras dos, podemos construir un romboedro que ocupará una fracción del interior del icosaedro. en este caso 3/20.

Si logramos llenar de forma semejante el resto del poliedro, habremos puesto los fundamentos para ocupar todo el espacio. porque en cada vértice exterior podremos repetir el procedimiento, como hicimos para llenar el plano con los con los rombos de Penrose.

Esta es la misma figura desde otro punto de vista. En la parte inferior de la imagen se comprueba la coincidencia de una cara rómbica con un plano de simetría del icosaedro.

Los rombos son naturalmente idénticos, y esta es precisamente la propiedad que permite adosar dos romboedros. Estas son sus medidas, y comprobamos que, como corresponde a figuras derivadas del pentágono, en todas aparece el mágico número F, el número de oro:

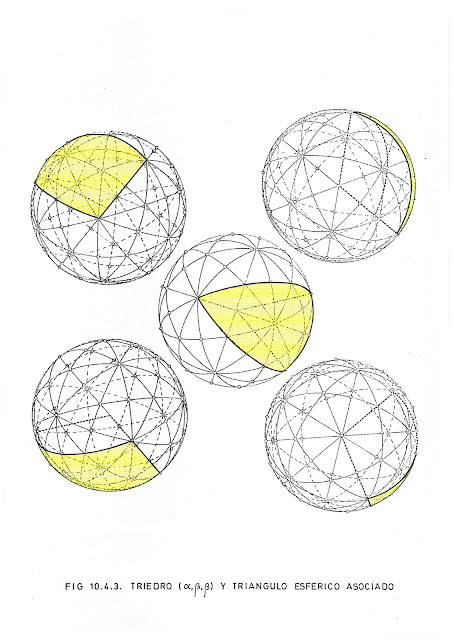
Procede analizar, proyectando sobre una esfera concéntrica el icosaedro y sus 120 módulos elementales (seis triángulos rectángulos por cada cara), qué porción ocupan sobre la superficie las caras de los triedros que pueden formar romboedros, habida cuenta de que, como ya hemos visto, esas caras corresponden a planos de simetría que contienen cada uno dos vértices, y no hay muchas posibilidades diferentes para elegir.

Así, si los tres vértices son contiguos, ocuparemos 6/120 = 1/20, o una cara:

Si elegimos un vértice y dos contiguos a él que no lo sean, ocupamos también seis módulos o dos medias caras, igualmente 1/20 de la superficie total:

Con dos vértices contiguos y un tercero alejado de ambos, pero no opuesto a ninguno de ellos, se ocupa una cara completa y cuatro medias caras del icosaedro, 18/120 = 3/20 de su superficie. Es el caso que hemos considerado antes:

Finalmente, con tres vértices no contiguos ni opuestos se ocupan cuatro caras completas y seis medias caras. En total 7 caras o cuarenta y dos módulos, 42/120 = 7/20.

Continuaré tratando de encajar estas piezas. Mientras, podéis seguir encajando los triedros entre sí y los romboedros en ellos.

(sigue)