La expresión gráfica en la ingeniería (12-a)

¡Toma Candela!

Estas delgadas cáscaras de hormigón de Félix Candela pueden cubrir grandes superficies a pesar de su ligereza, pues tienen muy pocos centímetros de espesor. El secreto es su forma. Son paraboloides hiperbólicos. En cada uno de sus puntos se cortan dos rectas. Si se disponen armaduras de acero en sus direcciones respectivas soportarán tanto esfuerzos de tracción como de compresión. Las barras en una dirección impiden el pandeo de las dispuestas en la otra. La  estructura es muy rígida, y no puede deformarse sin romperse.
 

En cada punto de una superficie continua existe un plano tangente y una recta normal, perpendicular a él. En los puntos elípticos el plano no corta a la superficie, al menos en un cierto entorno. En los hiperbólicos la corta en dos partes, una a cada lado del plano, y los cortes son líneas del plano tangente.

Si la superficie hiperbólica es doblemente reglada, hay dos familias de rectas sobre ella, una de cada familia por cada punto. Se trata entonces de una cuádrica reglada, como los paraboloides de Candela. 

Sigue esta serie con un nuevo capítulo, que puede descargarse en un documento PDF aquí, complementando el anterior con nuevos ejemplos.

Las superficies que siguen están definidas por tres directrices lineales, no necesariamente rectilíneas, aunque las que no lo son, en estos ejemplos, se han elegido planas y para mayor sencillez circulares o elípticas. Todas las generatrices cortan a las tres directrices. Comenzamos con esta, que ya se ha visto, y que sería un hiperboloide hiperbólico si no le hubiésemos "retorcido la garganta" hasta aplastársela (perdón por la crueldad metafórica).

La que sigue es una superficie uniaxial, porque una de las directrices es una recta. Para trazarla cortamos las elipses con planos que contengan al eje y unimos los puntos de intersección con ellas:

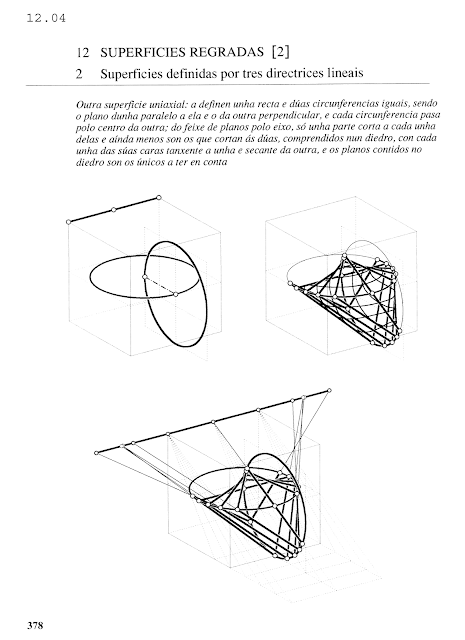
Otra superficie uniaxial. Utilizamos el mismo procedimiento para obtener generatrices, aunque ahora no todos los planos del haz cortan a las dos circunferencias:

Cosa que también ocurre en este otro ejemplo:

Esta otra superficie es biaxial, porque los ejes son dos. Cualquiera de ellos vale para trazar el haz de planos que corte a las otras dos líneas. Ahora es un tetraedroide. Los cartones de tetrabrik utilizaban algo semejante a esto, muy fácil de construir pero difícil de apilar. Por eso abandonaron la forma (aunque no el nombre) por el ortoedro actual de los paquetes de leche y del vino barato. Aún existe para algunos estuches de azúcar que me dan con el café.

En esta otra superficie biaxial hemos llevado la circunferencia fuera del recinto limitado por las dos rectas. En realidad, cualquier plano paralelo a ambas corta al tetraedroide en una cónica. Todos estos tetraedroides son idénticos, salvando el tamaño y que pueden estar más o menos aplastados.

Si nos vamos llevando cada vez más lejos esos planos paralelos, aparecen nuevas intersecciones que son elipses cada vez más alargadas... Pregunta: ¿cómo se proyecta esta superficie sobre el plano del infinito?

Esta otra superficie es triaxial. Las tres directrices son rectilíneas. Si existe un plano paralelo a las tres se tratará de un paraboloide hiperbólico, de esos de Candela.

Aquí no hay un plano paralelo a las tres, porque cada una es perpendicular a los planos paralelos a las otras dos: las tres se cruzan ortogonalmente

Tres vistas, en una de las cuales hemos puesto de punta una de las directrices. Así quedan de canto los planos del haz que sirve para obtener las generatrices que se apoyan también en las otras dos

La misma construcción en otro caso:

Para obtener la sección plana de una superficie cualquiera, en este caso reglada, pero vale para todas, cambiamos el punto de vista para poner de canto el plano secante. Con otro cambio más estará de frente.

Las secciones de rectas por un plano de canto determinan puntos. De ahí que sea tan fácil obtener secciones planas de superficies regladas.

Y basta por el momento.

(continúa)