Las diferentes circunferencias que percibimos en esta fotografía de la plaza de toros de Ronda aparecen en ella como curvas diferentes de lo que sabemos que realmente son. Algunas como elipses; otras son hipérbolas, y seguramente una es una parábola.
Todo depende del lugar desde donde ha sido tomada. Supongamos que desde la primera fila de barreras; entonces la imagen de esa fila es la dicha parábola. La barrera que separa el ruedo del callejón podría aparecer completa si el encuadre fuera más amplio, porque "la vemos toda" desde esta localidad, y esa curva entera (la superior, porque parte de la otra está oculta y solo un arco se deja ver) es una elipse. En cambio, de las cornisas de las arquerías solo podemos ver una parte, porque otra queda a nuestra espalda; lo que se ve es una rama de hipérbola. Con un ojo suplementario en la nuca veríamos las dos ramas.
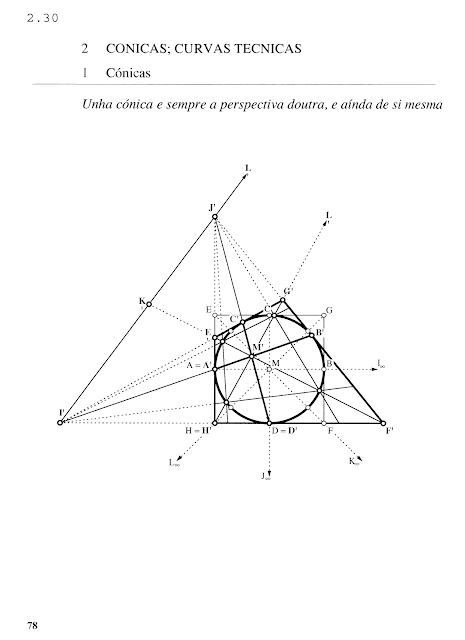
Partimos de lo que ya sabemos sobre la polaridad en las cónicas, considerando que en las figuras representativas del triángulo autopolar se podían percibir perspectivas de la circunferencia, y de qué manera los elementos del cuadrado circunscrito configuran cuaternas armónicas. Vamos ahora a dibujar esas curvas como perspectivas. Los distintos cuadriláteros serán las plantillas para trazarlas.
En todas las construcciones utilizo la misma nomenclatura para los puntos del cuadrado, bien fácil de recordar: A, B, C, D son los puntos de tangencia con la circunferencia, puntos medios de los lados del cuadrado; E, F, G, H, son sus vértices; I, J, los puntos del infinito de AB y CD; K, L, los de las diagonales; por último, M es el centro del cuadrado y de la circunferencia.
Para obtener un punto cualquiera aprovechamos la propiedad de que los ángulos inscritos en una semicircunferencia son rectos. En la elipse usamos la construcción correlativa.
El rectángulo nos lleva a una elipse dada por sus ejes, y el paralelogramo en general a la que definen dos diámetros conjugados.
Si inscribimos la circunferencia en un cuadrado distinto, la misma transformación producirá otro paralelogramo. Lo que en la circunferencia es un giro del plano, para la elipse es otra transformación, en la que ella permanece fija, pero no así sus puntos.
He aquí dos perspectivas de la circunferencia. De nuevo, ella permanece estable en perspectivas de sí misma. Solo algunos de sus puntos permanecen en el mismo lugar.
En el primer caso los puntos A y B son fijos. En el segundo A, H y D permanecen en su lugar.
En estas otras figuras permanece fijo el punto A.
Estas transformaciones de unas figuras en sí mismas, conservanfo fijos algunos elementos son manifestaciones de lo que en geometría proyectiva se conoce como involución (sobre la involución y otras transformaciones hice en otros tiempos algunos trabajos que deben andar perdidos en publicaciones de los congresos de Ingegraf; si encuentro los originales y el tiempo y espacio necesarios los publicaré, pero bueno, es mucho pedir...)
Transformando el cuadrado circunscrito en un trapecio con base en el infinito, la circunferencia se transforma en parábola. Un punto de tangencia emigra al infinito, y una paralela media se convierte en eje de la curva.
Obtención de un punto empleando el método correlativo al usado en la figura 2.27 para la circunferencia. EM y PP, que eran allí paralelas, confluyen ahora en el punto de fuga K.
Ahora el cuadrilátero transformado es un trapezoide con un lado en el infinito. AB es una cuerda, y CD su diámetro conjugado.
La misma parábola admite las dos construcciones anteriores. A'B' es una cuerda, C'D' su diámetro conjugado. Todos los diámetros son aquí paralelos al eje.
Ahora el cuadrado se convierte en un cuadrilátero "roto", con dos puntos en el infinito; el vértice en que confluyen los lados en que se hallan es transportado al "más allá"...
Ahora transportamos al infinito (¡así de fácil!) los puntos de tangencia A y B. Ahora tenemos una cónica con dos puntos en el infinito: una hipérbola. CD es el eje real, KL el imaginario.
También aquí hay otras posibilidades para el cuadrilátero transformado y descoyuntado que producen la misma hipérbola.
Superposición de los dos cuadriláteros, permaneciendo fija la hipérbola, aunque no sus puntos, excepto los del infinito. Las asíntotas, naturalmente, se conservan.
Hiperbola definida por las asíntotas y un punto.
Hipérbolas conjugadas; comparten las asíntotas y el cuadrado circunscrito.
Las dos hipérbolas conjugadas en una sola imagen. Cuando los diámetros real e imaginario (se invierten entre sí para cada una) son perpendiculares, lo son también las asíntotas. Entonces se las llama hipérbolas equiláteras. Las hipérbolas equiláteras tienen sus asíntotas perpendiculares, y tomadas como ejes cartesianos representan la función proporcionalidad inversa.
En todo caso, estas hipérbolas conjugadas son perspectivas de las equiláteras.
Terminamos este capítulo con otras curvas. La primera, una parábola cúbica, es muy sencilla si su ecuación se representa gráficamente en coordenadas cartesianas. La segunda es una espiral logarítmica, de ecuación muy simple en coordenadas polares.
Y finalmente dos curvas cíclicas, curvas de rodadura, una cicloide y una epicicloide.
Culminado este capítulo, pasaremos al tercero.



















No hay comentarios:
Publicar un comentario